Deep Learning Book Notes
深度前馈网络deep feedforward network
基于梯度的学习——代价函数:
- 使用最大似然学习条件分布。大多数现代的神经网络使用最大似然来训练。这意味着代价函数就是负的对数似然,它与训练数据和模型分布间的交叉熵等价。
- 均方误差和平均绝对误差在使用基于梯度的优化方法时往往成效不佳,一些饱和的输出单元当结合这些代价函数时会产生非常小的梯度,这就是为什么交叉熵代价函数比均方误差或者平均绝对误差更受欢迎的原因之一。
基于梯度的学习——输出单元:
- 代价函数的选择与输出单元的选择密切相关。任何可用作输出的神经网络单元,也可以被用作隐藏单元。
- 用于高斯输出分布的线性单元:一种基于仿射变换的输出单元,仿射变换不具有非线性,所以这些单元往往直接被称为线性单元。
- 用于Bernoulli输出分布(伯努利分布)的sigmoid单元:许多任务需要预测而执行变量的值。具有两个类的分类问题可以归结为这种形式。
- 用于Multinoulli输出分布(多项分布)的softmax单元:任何时候当我们想要表示一个具有n个可能取值的离散型随机变量的分布时,我们都可以使用softmax函数。它可以看作是sigmoid函数的扩展,其中sigmoid函数用来表示二值型变量的分布。
隐藏单元:
整流线性单元及其扩展:整流线性单元易于优化,它与线性单元非常类似。线性单元和整流线性单元的唯一区别在于整流线性单元在其一半的定义域上输出为零。
logistic sigmoid与双曲正切函数:

其他隐藏单元:softmax单元,径向基函数(rational basis function,RBF),softplus函数,硬双曲正切函数(hard tanh)
深度学习中的正则化和优化
深度学习中的正则化:对学习算法进行修改,旨在减少泛化误差而不是训练误差。模型族训练有三个情形:
- 不包括真实的数据生成过程,对应欠拟合和含有偏差的情况;
- 匹配真实数据生成过程;
- 除了包括真实的数据生成过程,还包括许多其他可能的生成过程——方差(而不是偏差)主导的过拟合。
正则化的目标是使模型从第三种情况转化为第二种情况。
深度学习中的优化:用于深度模型训练的优化算法与传统的优化算法在几个方面有所不同。机器学习通常是间接作用的。在大多数机器学习问题中,我们关注某些性能度量P,其定义于测试集上并且可能是不可解的。因此,我们只是间接地优化P。我们希望通过降低代价函数J(θ)来提高P,这一点与纯优化不同,纯优化最小化目标J本身。训练深度模型的优化算法通常也会包括一些针对机器学习目标函数的特定结构进行优化。
卷积神经网络convolutional neural network
卷积神经网络,也叫做卷积网络,指那些至少在网络的一层中使用卷积运算(卷积运算是一种特殊的线性运算)来替代一般矩阵乘法运算的神经网络。这种网络是一种专门用来处理具有类似网格结构的数据的神经网络,比如时间序列数据和图像数据。
卷积运算:
s(t) = ∫x(a)w(t - a)da
上面这种运算称为卷积(convolution),卷积运算通常用星号*表示。
s(t) = (x * w)(t)
在卷积运算的术语中,卷积的第一个参数(上式中的x)通常叫做输入(input),第二个参数(上式中的函数w)叫做核函数(kernel),输出有时被称为特征映射(feature map)。
动机:卷积运算通过三个重要思想来帮助改进机器学习系统:稀疏交互(sparse interactions)、参数共享(parameter sharing)、等变表示(equivariant representations)。
池化:卷积网络中一个典型层包含三级。第一级中,这一层并行地计算多个卷积产生一组线性激活响应。第二级中,每一个线性激活响应将会通过一个非线性的激活函数,例如整流线性激活函数。这一级有时也被称为探测级。第三级中,我i们使用池化函数来进一步调整这一层的输出。
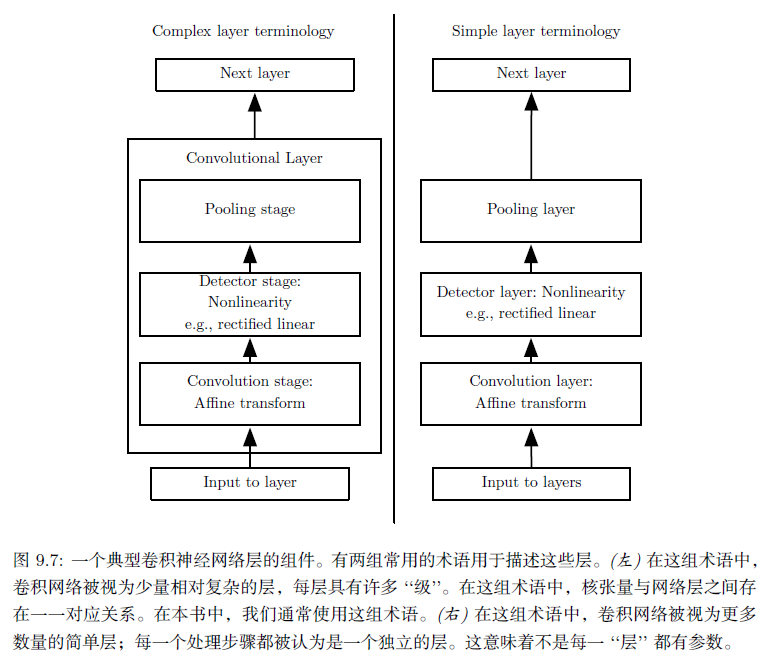
池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。
循环神经网络recurrent neural network
循环神经网络rnn:这是一类用于处理序列数据的神经网络。
循环神经网络中的一些重要的设计模式:
- 每个时间步都有输出,并且隐藏单元之间有循环连接的循环网络。
- 每个时间步都产生一个输出,只有当前时刻的输出到下个时刻的隐藏单元之间有循环连接的循环网络。
- 隐藏单元之间存在循环连接,但读取整个序列后产生单个输出的循环网络。
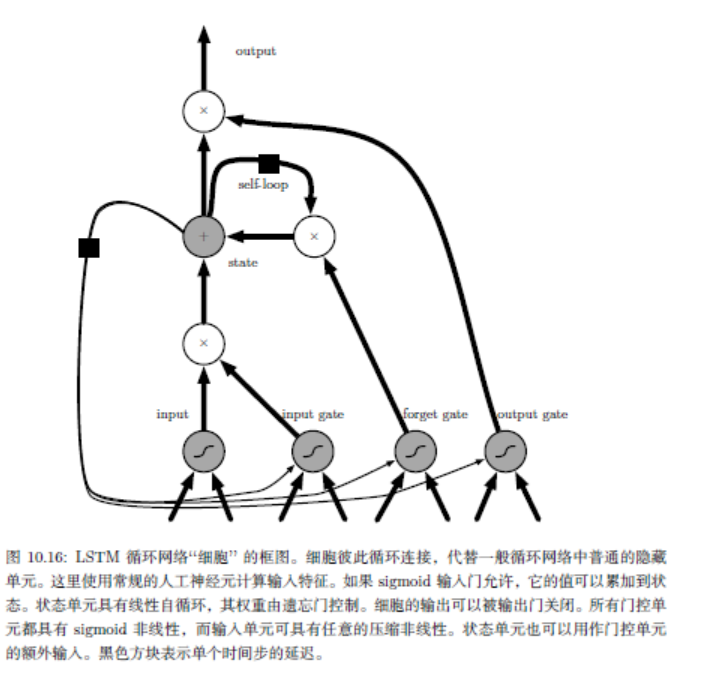
长短期记忆LSTM:引入自循环的巧妙构思,以产生梯度长时间持续流动的路径。